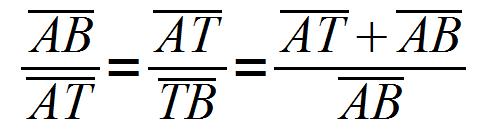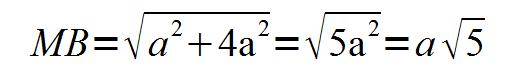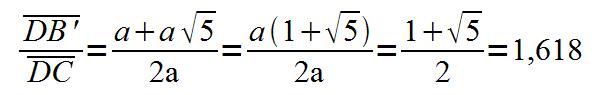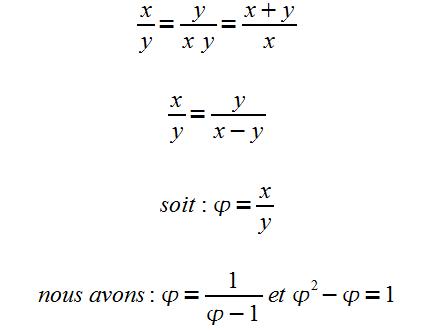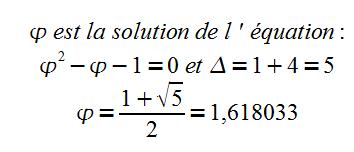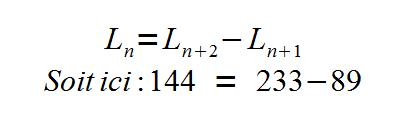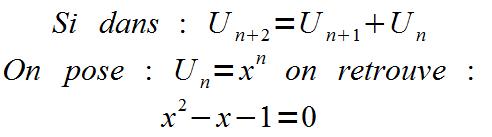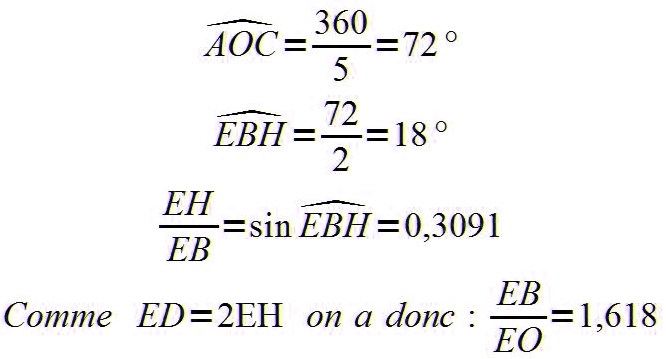(Auteur : Gaston FONTAINE, pour le Conotron)

Lorsque Prométhée descendit sur la terre où dans le ciel passaient les oiseaux, dans les prairies paissaient les troupeaux, dans les eaux nageaient les poissons, il chercha en vain les êtres vivants marchant comme lui et lui ressemblant. De la terre, sortaient de l’herbe, des plantes, des arbres qui poussaient grâce à l’eau qui tombait du ciel et au soleil qui y brillait.

Il en conclut que la vie se situait à l’intérieur d’un triangle aux dimensions égales et dont les sommets étaient l’eau, la terre et le feu et qu’en combinant ces trois facteurs, il pouvait faire un homme à l’image des Dieux: en mélangeant de la terre et de l’eau, et en faisant sécher la forme au soleil.

Pour faire l’homme à l’image des Dieux, encore fallait-il connaître leurs mensurations idéales. Pour ce faire, Prométhée réunit les Dieux Olympiens, Héra, Athéna, Apollon, Artémis, Arès, Héphaïstos et Aphrodite (une sculpture du musée de Naples reproduit la scène).

Prenant leurs mesures (avec un bâton à encoches) il constata que les corps des Dieux et Déesses obéissaient à la même proportion, à savoir l’égalité entre les rapports : ·       pieds-tête AB sur pieds-nombril AT ·       pieds-nombril sur nombril-tête ·       pieds-tête plus pieds-nombril sur pieds-tête

Ce que traduit la formule suivante :

Dieux et déesses étant d’accord pour l’application de ces mesures à la créature humaine, Prométhée mélangea de l’argile et de l’eau de pluie, moulant la forme du premier homme qu’il mit à sécher au soleil.

La forme étant sèche, Athéna, déesse de la sagesse et de l’esprit lui insuffla une âme, le coeur se mit à battre et les membres à bouger, et de joie la première créature humaine se mit à chanter.

Mais Prométhée avait, tout simplement, oublié de doter la forme d’un sexe apparent; aussi, Aphrodite, la pus belle des déesses qui règne sur l’amour et le désir et qui n’avait pas oublié que Cronos avait émasculé son père Ouranos, s’empressa, à l’aide d’une flèche qu’elle avait dérobée à Artémis, d’inciser l’entre-deux cuisses de la forme humaine, en en faisant une femme, lui transmettant sa beauté, l’amour et le désir.

Ce qui conforte l’affirmation des féministes: le premier homme était bel et bien une femme – qui commença à se reproduire en se mirant dans l’eau de la rivière du Dieu-fleuve Asopos.

Il fallut attendre Priape, fils d’Aphrodite, pour que donnant un peu de lui-même et de son âme, il rectifia l’erreur de sa mère en dotant la femme de ce qu’il lui manquait pour en faire un homme.

Certaines refusant la monstruosité de la chose, se refusèrent aux hommes pour se satisfaire entre elles et certains hommes se voyant refusés des femmes, firent de même entre eux. Ce qui serait à l’origine de l’homosexualité.

C’est Euclide d’Alexandrie qui, en 300 avant Jésus-Christ, utilisa la géométrie pour identifier ce qu’on appela la « divine proportion » ou Nombre d’Or.

Si, utilisant dans un carré, l’axe de symétrie, on en fait deux rectangles. Quelque soit ce carré, la moitié d’un côté du carré plus l’hypothénuse d’un de ces rectangles, rapporté à un côté de ce carré, est égal au nombre d’or.

Démonstration:

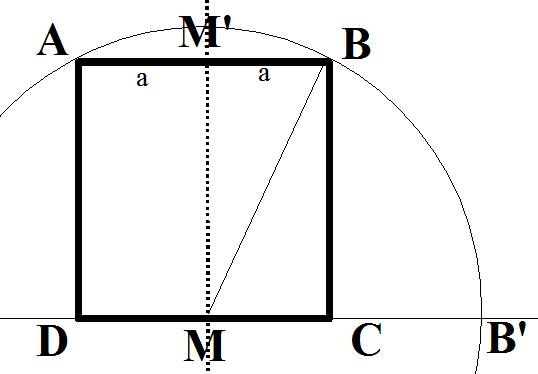Soit un carré ABCDdont l’axe de symétrie est noté: MM’ et où « a » est égal à la moitié d’un côté.

En appliquant le théorème de Pythagore au triangle rectangle BCM dont le petit côté vaut « a » :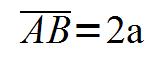 

D’où le nombre d’or : 

En développant le calcul, on obtient :

Φ = 1,618033988749

Par la suite, un rectangle d’or a été défini, dont les côtés sont dans la proportion du nombre d’or, ou encore comme un rectangle dont la différence des carrés de ses dimensions est égale à sa surface. Soit avec un côté noté a et un côté noté b, pour lequel a > b, on aura: a² – b² = ab

Le visage de la Joconde s’insère dans un rectangle d’or. En prenant une représentation du tableau dans un ouvrage, on peut mesurer la hauteur: 8,9 cm et la largeur: 5,5 cm

(8,9)² – (5,5)² = ab

79,21 – 30,25 = 48,96

ab = 8,9 . 5,5 = 48,95

avec 8,9 / 5,5 = 1,618181818

Le David de Michel-Ange se conforme aux proportions du nombre d’or et rentre dans le rectangle. Il en est de même pour le Parthénon d’Athènes dont la façade pourrait s’encadrer dans un rectangle d’or.

De fait, il fallut attendre l’invention de l’algèbre par Al Kharezmi (Livre abrégé du calcul par l’al-jabr et la muquabala, vers 750) pour calculer algébriquement le nombre d’or à partir des données de Prométhée.

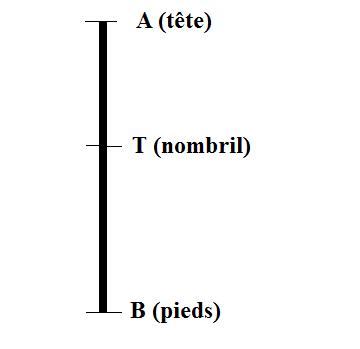
Soit x la taille de l’individu et y la hauteur des pieds au nombril :

1ère donnée : 

2ème donnée :

Extension du Nombre d’Or :

1) La suite de Fibonacci (1170 – 1240).

Le mathématicien Fibonacci, bien que brillant, était tombé dans l’oubli. Il y serait sans doute resté si Edouard Lucas, arithméticien français (1842 – 1891) ne s’était pas penché sur le problème des lapins, que Fibonacci avait voulu résoudre pour s’amuser.

« Si je place dans un enclos, un couple de lapins, combien aurai-je de lapins au bout de douze mois, sachant qu’un couple de lapins ne peut copuler qu’à partir du second mois de sa naissance et qu’il engendre chaque mois un nouveau couple »

 Il suppose que les lapins ne meurent pas et que tout couple de lapins n’est fécond qu’à partir du deuxième mois de sa vie. Il note Ln : le nombre de couples au début du mois et écrit la suite:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, etc

A la fin du douzième mois, il y aura 233 couples soit 466 lapins et lapines. En examinant cette suite on peut écrire :

On constate également que le rapport entre deux termes consécutifs tend vers le Nombre d’Or. Par exemple: 89/55 = 1,618   De même: 987/610 = 1,61803

Mais quelle relation tout ceci a-t-il avec la création de l’homme ?

Lorsque Prométhée forma le premier homme, ou plutôt le premier être humain, Héra la déesse du mariage et de la famille lui demanda de sa voix peu suave: «  Comment cette créature va-t-elle se reproduire? » Prométhée hésitait à répondre, lorsqu’un lapin lui déboucha entre les jambes: « Eh bien, comme les lapins ! » Et il ajouta: « Dans les mêmes proportions que ses mensurations… ».

Aphrodite rectifia aussitôt : « Lorsqu’elle sera en couple, il faudra tenir compte des méfaits de Thanatos, le Dieu de la Mort, et limiter sa fécondation au quart de la longueur du jour… »

En effet, dans sa suite, Fibonacci avait supposé que les lapins ne mouraient jamais ou n’étaient jamais mangés. Si Aphrodite est à l’origine de la guerre de Troie, du siège de dix ans qui s’y déroula et où les hommes se bouffèrent entre eux, on n’a encore jamais entendu parler de la guerre des lapins.

Sur une longue période, on calcule qu’avec un taux de mortalité situé entre 26 et 32%, le taux de fécondité pour le maintien de la population devrait se situer entre 2,06 et 2,12%

Or on constate que le rapport entre taux de fécondation sur taux de mortalité est de 2,09 / 1,29 soit 1,620, très proche de 1,618. De plus, sur la tranche d’âge des femmes de 83 ans, le nombre de femmes survivantes sur 1000 nées la même année est de 61804; soit 61804 / 100000 égal à 1,618. Au même âge de 83 ans, il y a 38195 hommes; soit un rapport de 61804 / 31895 égal à 1,618. Partout, on retrouve le Nombre d’Or.

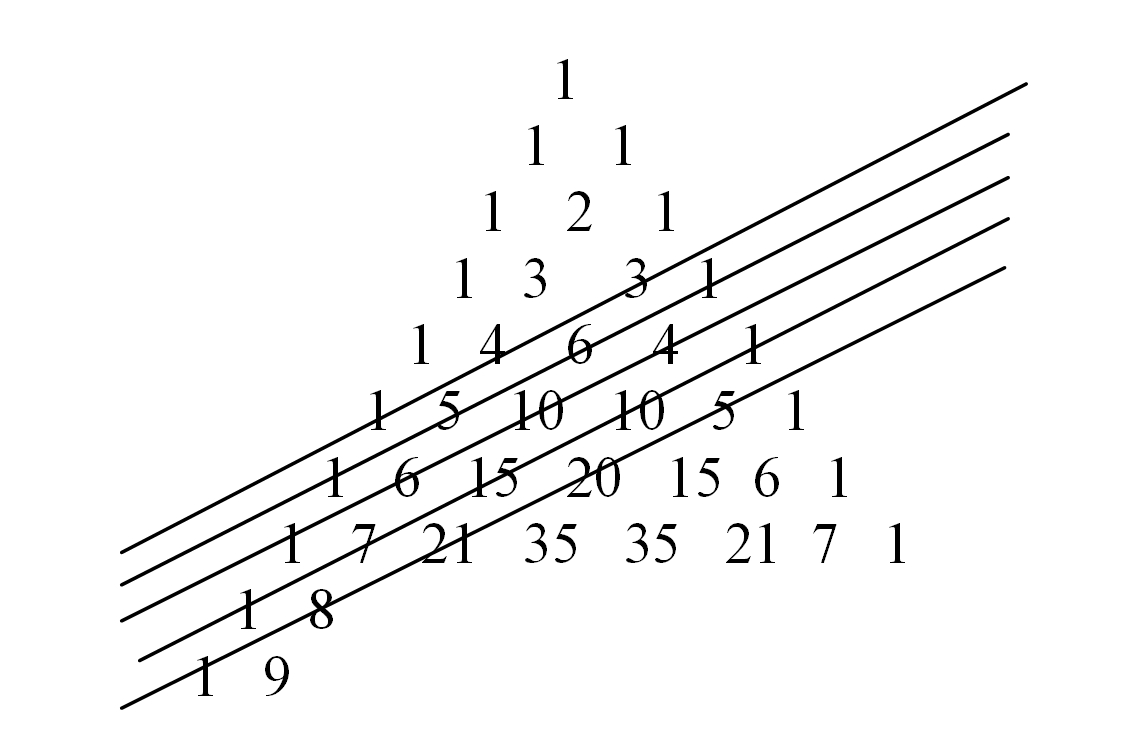
Dans le domaine des probabilités, on remarque que dans le triangle de Pascal, la somme des nombres en diagonale correspond aux nombres de Fibonacci : 8,13,21,34,55,etc

 

On peut chercher à établir, à partir de la relation citée, une expression fonctionnelle :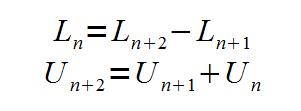

Les suites de ce type sont des « combinaisons linéaires » et on peut trouver deux suites « géométriques » qui vérifient cette relation. C’est le cas de la suite d’Edouard Lucas :

1, 3, 4, 7, 11, 18, 29, 47, etc

et là encore: 123/76 = 1,618

Ceci définit « algébriquement » le Nombre d’Or, comme un Réel positif dont la différence avec son propre carré est égal à 1.

 

2) Le Pentacle

Le Pentacle est l’un des premiers symboles connus de l’être humain. Sa forme est l’étoile à cinq branches, dotée de bras équilatéraux et d’angles égaux à chacune de ses cinq pointes.

Il était connu comme celui de Vénus, la planète Vénus traçant un pentacle dans le ciel étoilé, pendant six ans. En effet, selon les Anciens, si pendant six ans, le même jour, on observe Vénus par rapport aux étoiles et que l’on trace sa trajectoire sur une feuille de papier, on obtient un pentacle.

Les Pythagoriciens l’identifiaient à Hygie, la déesse grecque de la santé. Pour certaines sectes, il est un symbole.

Or, le rapport entre la branche du pentacle et le côté du pentagone inscrit dans le cerce est égal au Nombre d’Or. On peut facilement tracer le pentacle à partir du triangle inscrit (triangle isocèle: dont le rapport entre les côtés est égal à 1,618 soit le Nombre d’Or). Exemple: soit un triangle dont la base est de 6 cm, tracé à l’aide d’un compas et d’une règle graduée. Son côté est de 6 * 1,618 soit 9,7

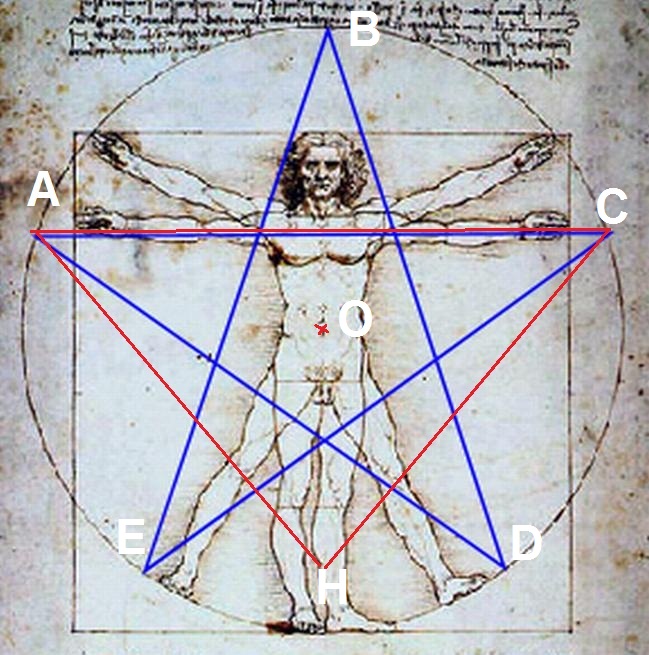
L’homme de Vitruve, dessin de Léonard de Vinci, inspiré par l’étude de Marcus Vitruvius (architecte du 1er siècle avant Jésus-Christ) s’inscrit dans un pentacle.

Les proportions de l’homme de Vitruve correspondent au Nombre d’Or.

Démonstration : 

3) L’extension au domaine des cons

Dans son livre « Propos d’O.L Barenton, confiseur, ancien élève de l’Ecole Polytechnique », Auguste Detoeuf écrivait: « De quelque façon et par quelque moyen qu’on décompose une collectivités en groupes, choix, ancienneté, concours, examens ou tout simplement tirage au sort, dans les divers groupes, la proportion de cons est toujours la même. »

Son éditeur, sans lui demander son avis, remplaça « cons » par « imbéciles ».

Il avait tort, l’éditeur, car si l’imbécilité peut se mesurer grâce au quotient intellectuel, QI < 30, la connnerie, quant à elle, est incommensurable, faute d’avoir trouvé une valeur de référence.

Il est évident que le con existe, notre Président de la République en a rencontré un « pauvre » et comme le confirmait un de ses proches ministres: « S’il n’y en qu’un en France, c’est bien celui-là ».

Un professeur de mathématiques, admirateur d’Auguste Detoeuf – les « Propos d’O.L Barenton » était son livre de chevet – et qui s’était penché sur les étonnantes propriétés de la suite de Fibonacci et donc du Nombre d’Or, se posa la question: si la Divine Proportion est bien un paramètre essentiel dans la nature comme on le constate aisément, dans les inflorescences du tournesol qui possèdent souvent 89 et 144 spirales, soit 144/89=1,618 , dans la longueur d’une spirale d’ADN par son diamètre, de même pour la coquille d’un mollusque, et, allant retirer de l’argent à un distributeur automatique, il eut l(idée de mesurer sa carte de crédit. Alfred Beiche, qui aimait remuer le cie et la terre pour trouver la solution aux problèmes qu’il se posait eut l’idée de mesurer sa carte « Visa » avec précision, il utilisa pour ce faire un pied à coulisse et son ordinateur et constata qu’effectivement le rapport L/l donnait exactement: 1,618033988749894 Ce qui exactement le Nombre d’Or en valeur approchée, son esprit d’agrégé ne fit qu’un bond. Il était évident que la proportion de cons obéissait au Nombre d’Or. Fallait-il considérer cela comme un « axiome », un « postulat », ou fallait-il le démontrer ?

Alfred qui donnait son « bonjour » à tout le monde, avait pensé les résultats qu « quotient intellectuel » de Stanford-Binet qui, théoriquement, obéit à la courbe de Gauss f(t) et à sa fonction intégrale :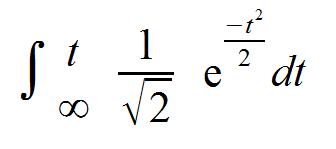Sur la table de la fonction, on peut constater que pour tout : t < 0,3 on trouve 0,6179 qui n’est ni plus ni moins que l’inverse du Nombre d’Or et qui signifierait qu’en pondérant les calculs sur 1000 individus, il y aurait 617 cons.

Mais attention ! Il est avéré que l’intelligence ou la connerie peuvent se présenter sous bien des formes, un sujet peut se montrer intelligent sous un aspect et parfaitement con sous un autre.

C’est ainsi qu’en fouillant la pensée de Detoeuf, Alexandre put noter qu’un individu prit au hasard peut être :

• intelligent et con (sans bon sens)
• Peu intelligent, peu instruit mais pas con (possédant du bons sens)
• Inintelligent, pas instruit (nul et sans bon sens, un débile)

 En première approximation, la connerie et le bon sens peuvent-ils être confondus?

 On se souvient qu’un Président de la République, ancien élève lui aussi de l’Ecole Polytechnique et doté d’un QI >150 c’est à dire exceptionnel, s’était fait avoir avec les « avions renifleurs de pétrole ». Un de ses camarades de promotion s’était écrié: « C’est pas possible d’être aussi con! »

Connerie = Intelligence – Bons sens

La femme dite « de ménage » d’Alfred, avait pour compagnon un caporal-chef parachutiste, de carrière, qui distribuait les tests aux jeunes convoqués lors de la journée d’appel de préparation à la défense. Albert, c’était son nom, n’était pas diplômé, mais loin d’être con. Il n’avait pas trouvé en fin de terminale dans la pochette surprise délivrée par l’Education Nationale, le papier tant désiré, sa calculatrice étant tombé en panne lors de l’épreuve de mathématiques. Albert était sans grande prétention, il aurait voulu comme son père ancien adjudant-chef, faire une carrière de sous-officiers, mais sans baccalauréat, pas d’entrée possible à ‘Ecole des Sous-off’.

 Aussi Alfred eut l’idée de demander à Albert, de glisser au milieu des tests dits « officiels », ses tests à lui, Alfred, les fameux « bloody non-sense tests » sous forme de Q.C.M du type :

« Vous vous êtes absenté(e) quelques jours et vous rentrez chez vous plus tôt que prévu, sans avoir eu la possibilité de prévenir votre compagne/compagnon. En entrant vous criez: chéri(e) c’est moi!, vous entendez alors quelque remue-ménage dans la chambre, vous y pénétrez, allumez et vous apercevez, sortant de dessous les doubles rideaux de la fenêtre, deux pieds nus, alors que votre compagne/compagnon fait sembant de dormir.

Quelle est votre réaction?

□ Je dis à ma compagne/mon compagnon, ah, je suis en sueur, je vais prendre une douche. Afin de permettre à l’intrus(e) de s’en aller sans esclandre.

□ J’ouvre les doubles rideaux et je félicite l’inconnue(e) pour son bon goût et je le remercie de me donner l’occasion de me débarrasser de l’emmerdeur(euse) qui empoisonne votre vie.

□ Je ferme la porte d’entrée à double tour en gardant la clé, et j’appelle la police en leur disant que quelqu’un de suspect s’est introduit chez moi.

□ Sans objet

Les réponses étant notées de 0 à 1, le meilleur dans le domaine de la connerie était en droit d’obtenir la note maximale. Alfred, concentré il faut le dire, rédigea 75 tests chacun de 50 questions. Albert n’eut aucun mal à extraire de la masse des papiers, les tests d’Alfred, il avait tout son temps. En effet, ses supérieurs estimaient que la « journée d’appel » était une vraie connerie, inventée par ces cons de civils qui nous gouvernent, et s’en foutaient complètement. On restait bien dans le dit domaine.

Albert étant rémunéré à coup de packs de Kronenbourg, n’hésita pas à accepter de renouveler l’opération.

C’est ainsi que 1429 tests furent examinés, après avoir éliminé les « sans-objet » et les griffonneries considérés comme « abstentionnistes », il en resta 883 exploitables. Soit 1429/883 = 1,618 ou encore 1429 – 883 = 546/1429 soit 38% disons d’abstention, ce qui nous rappelle le pourcentage moyen des élections et nous interpelle sur la réponse d’un de nos acteurs préférés ou censé l’être: « Je ne vais jamais voter, y a que les cons qui y vont. »

Ce qui corrobore le jugement fait sur l’abstention du « pauvre con » qui n’avait sûrement pas voté pour notre Président bien-aimé.

La différence entre la meilleure note obtenue: 9,30 et la plus basse: 5,75 correspondait bien au Nombre d’Or: 9,30 /5,75 = 1,617.

Tous ou toutes ayant obtenu une note supérieure à la moyenne, on pouvait donc conclure qu’il n’y avait que les cons et les connes pour avoir répondu.

Alfred comme tout scientifique voulut aller plus loin, afin de conforter sa certitude. Aussi, il demanda à une société de sondage de poser la question suivante à des personnes prises au hasard sur un bottin, choisi lui aussi au hasard: « Estimez-vous que la vie que vous menez est une vie de con? »

Cette opération étant coûteuse, on se contenta d’interroger un échantillon, mais en tenant compte de « l’intervalle de confiance » au seuil de 95% (soit 0,95 = deux écarts-types). Le résultat fut sans appel: 61,803% des répondants affirmaient qu’ils menaient une « vie de con »

 Notre vie est conditionnée par le Nombre d’Or et incontestablement, à l’heure actuelle, les cons dans notre société sont en majorité. Alfred appris sans aucune surprise que dans sa faculté, depuis cinq ans, 39% seulement des étudiants décrochaient leur diplôme de licence en trois ans, soit 61% de cons.

Un doctorant qui travaillait sous la coupe d’Alfred lui demanda: « Les Anciens étaient-ils aussi cons que nous?

– Tout ce que je sais, répondit Alfred, c’est que Cicéron en 75 avant Jésus-Christ écrivait : « Tria erant genere hominis: stolidus, silentus, callidus. » (Il y a trois sortes d’hommes: les cons, les silencieux et les rusés ») et il ajoutait, ce sont les rusés, les moins nombreux qui profitent du plus grand nombre. Il n’en précisait pas la proportion. »

Nous vivons actuellement dans un « monde publicitaire », il suffit d’ouvrir la télé pour s’en rendre compte. « Une publicité efficace disait un spécialiste de la chose, c’est celle qui fait acheter de la merde après avoir convaincu le consommateur que c’était de la crème au chocolat. Ou d’arriver à persuader le dit consommateur qu’un produit parfaitement inutile, lui est absolument indispensable. »

En tout état de cause, le Nombre d’Or est là et 39% ne s’y laissera pas prendre.

Mais, comme tout vêtement doit parfaitement s’adapter sur celui ou celle qui le porte, la publicité doit s’adapter aux futurs clients: elle doit être con ! Plus elle est con, plus elle est efficace et elle se doit d’être con, car sans publicité pas de ventes possibles et si pas de ventes, pas de croissance.

Il en est de même de la politique. Pour être élu(e) il faut une « campagne con », raconter des conneries: « Du travail facile pour tous et toutes, des revenus confortables, le restaurant deux fois par mois, au minimum un domicile agréable, des vacances à la neige et au soleil… »

Et un « loin-d’être-con » est élu. Il continue à prendre le peuple pour un ensemble de cons, toujours selon le Nombre d’Or : 61%

Les cons s’apercevant qu’ils se sont conduits comme des cons, manifestent leur mécontentement. Ce qui fait crier aux forces de l’ordre « Mort aux cons » et personne ne peut s’étonner qu’il y en ait des deux côtés. On casse des cons, ou les cons – jeunes ou non – se cassent, en laissant tout cassé.

Le Nombre d’Or, qu’on lui soustrait 1 pour avoir l’inverse ou qu’on lui ajoute 1 pour avoir le carré, restera toujours ce qu’il est. Et même si l’on n’a jamais pu résoudre la quadrature du cercle, il est évident qu’un carré de cons, peut toujours être encerclé par un ensemble de semblables.

Comme le déclarait une de nos politiques: « Notre société de consommation a perdu son caractère humain, combattant les aspirations fondamentales de l’homme et de la femme à la spiritualité, à l’intellectualité, à l’art, à la beauté, à la poésie et en libérant la sexualité, a contribué à la prolifération des cons. » Un opposant aurait dit: « En tout cas, on ne touchera pas au sien, avec sa gueule personne n’en aura l’idée. » On peut se rassurer : il s’agit simplement du mari de l’élue.